Low rank factorization of Coulomb integrals

Reducing complexity

One of the most expensive steps in a canonical coupled cluster calculation is the particle-particle contraction of the amplitudes with the Coulomb integrals scaling as $\mathcal O(N^6)$. For larger systems this part of the integrals cannot even be kept in memory and needs to be computed on the fly.

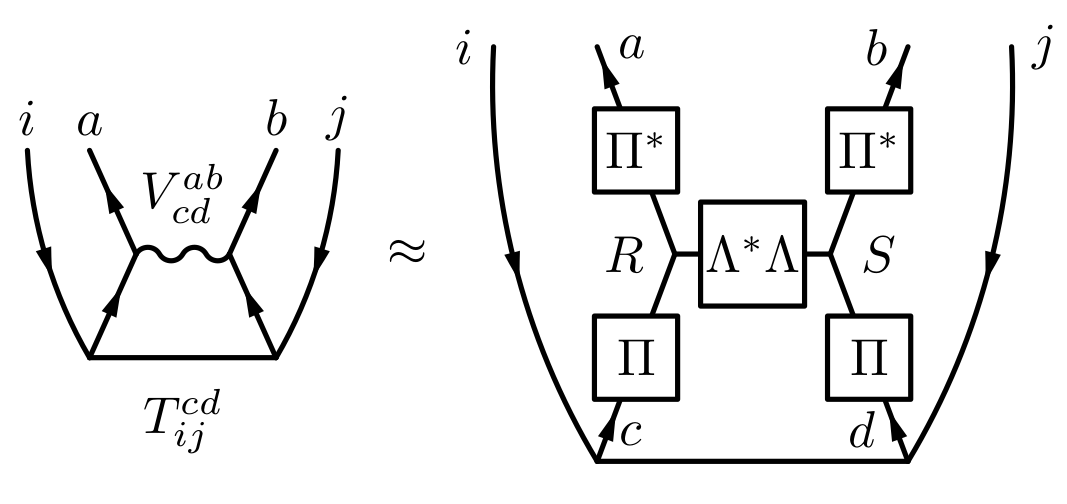
When factorizing the Coulomb integrals into a product of matrizes of which only 2 are distinct, the complexity of above contraction reduces to $\mathcal O(N^5)$. The factorization ansatz is motivated from the real space definition of the integrals and it is known under the name Tensor Hyper Contraction. The factorization is, however, difficult to compute despite its comparatively low formal complexity of $\mathcal O(N^4)$. We employ a modified regularized alternating least squares fit to determine the factorization, lowering the overall computation times of CCSD by an order of magnitude.