Electronic Structure at Finite Temperature
Coupled Cluster theory
In warm dense matter electronic correlation is comparable to the thermal fluctuations $k_\mathrm B T$. It is found in gas giants but also in metals. Accurately describing quantum mechanical correlation in thermal systems poses a difficult problem which we try to tackle by generalizing coupled cluster methods from zero temperature to finite temperatures. [1,2]
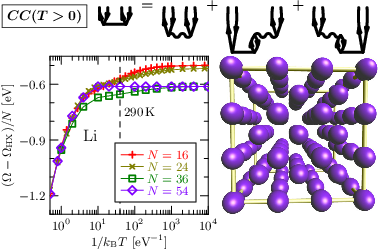
Figure 1: Correlation grand potentials for Lithium for various super-cell sizes in the linearized direct ring coupled-cluster doubled (ldrCCD) approximation. The theory allows for very low temperatures and is thus suitable for metals.
We aim at the study of electronic temperature effects in reactions, such as high pressure solid-solid phase transitions or the heterogeneous catalysis on metal surfaces. We also study the warm electron gas to complement the development of approximate finite temperature exchange-correlation functionals, especially in the region, where Monte Carlo methods are less accurate.
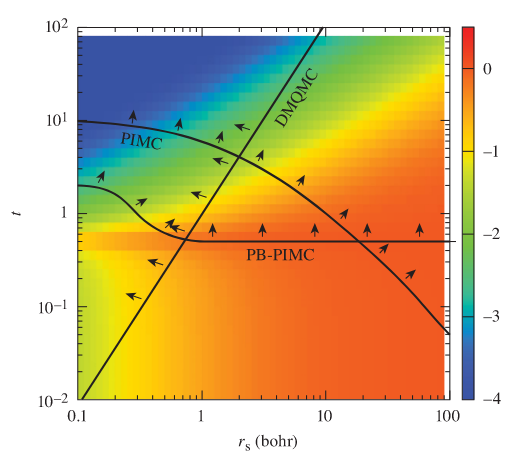
Figure 2: Magnitude $\log_{10}\big({|f_\mathrm{xc}|}/(|f_\mathrm{s}|+|f_\mathrm{xc}|)\big)$ of the exchange-correlation contribution in the phase space of the uniform electron gas. The arrows point towards the regions where the various Monte Carlo techniques are accurate: Path Integral Monte Carlo (PIMC), Permutation-Blocking PIMC (PB-PIMC), Density-Matrix Quantum Monte Carlo (DMQMC). The low-temperature and intermediate-density region is important for applications but not well described by Monte Carlo methods. Figure from [3]
[1] White and Chan, J. Chem. Theory Comput. 14(11), 5690-5700 (2018).
[2] Hummel, J. Chem. Theory Comput. 14(12), 6505-6514 (2018).
[3] Karasiev, Trickey, and Dufty. Phys. Rev. B 99, 195134 (2019)
